by David Wilcock from Ascension2000 Website recovered through WayBackMachine Website We have indeed seen the evidence to suggest that the atom is an aether-vortex with spherical symmetry and a central axis, thus forming a spherical torus. The Biefield-Brown effect proves that the grand solution to the mystery of “charge polarity” is that aetheric energy is flowing through the electron clouds into the nucleus. Dr. Ginzburg made a few simple and acceptable adjustments to relativity equations and produced a model that perfectly explains the behaviors of matter observed by Kozyrev in the laboratory, wherein it sheds energy and mass as it is accelerated towards the speed of light.
We can no longer deny that these forces exist, as we now have irrefutable physical evidence. These new findings also reveal that we no longer need to think of atoms as individual units, but rather as harmonic aether vortexes that can merge together into greater levels of unity and coherence, such as in quasi-crystals. And with this data in place, we now have a valid solution for all the “loose ends” of the puzzle by introducing the work of Rod Johnson.
Significantly, an increasing number of advanced theorists have already been striving towards a “particle mesh” model of physics, based on the Superstring theory, where all matter in the Universe is somehow an element of an interconnected geometric matrix. However, since conventional scientists have not yet visualized Platonic Solids that are nested within each other, sharing a common axis and capable of counter-rotating, they have missed the picture for the quantum realm.
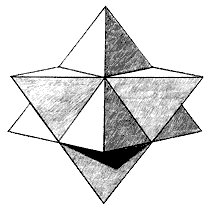
We begin our outline of the core principles of the model with a pencil-shaded illustration of the interlaced tetrahedron, which we created to show very clearly what it looks like as a three-dimensional sculpture. It is important that we have a good visual image of this structure before we try to imagine an octahedron that fits inside of it. We can clearly see that there are two tetrahedrons in the image, one with the tip pointing upwards and another with the tip pointing downwards. Also remember that it fits perfectly inside a sphere:
Figure 4.1 – The interlaced tetrahedron. "click" image for animation With this structure in mind, consider the following points of the model:
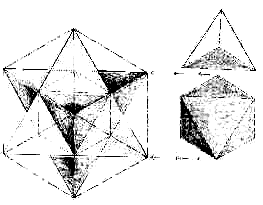
Figure 4.2 – The octahedron (R) and its fit inside the interlaced tetrahedron (L). [Lawlor, 1982]
Figure 4.2 shows us the octahedron inside of the interlaced tetrahedron, which in turn is inside the cube. It is quite confusing at first to try to imagine the octahedron being a free agent that can counter-rotate inside the interlaced tetrahedron. Indeed, in this form, the two geometries are completely balanced and integrated. However, the most important part of Johnson’s physics is to see that the octahedron is “detached,” acting separately from the tetrahedral field, by rotating in the opposite direction. There are only eight possible “phase” positions that the two geometries can fit into before they again reach the harmony that we see above. In order to have a phase position, the two geometries must have some degree of direct contact with each other, such as line to line or point to point. This is graphically illustrated in the next “phase” diagram:
Figure 4.3 – The eight “phase positions” created by the counter-rotating octahedron and tetrahedron.
What we see in this diagram are two basic waves: the smaller wave that fits in each of the four main circles, representing the rotation of the octahedron, and the larger wave outside the main circle boundaries as the counter-rotation of the tetrahedron. This diagram is by far the easiest way to show how and where the tetrahedron and octahedron will connect, and it is based on the science of “phase physics,” which was first pioneered by Kenneth Geddes Wilson as a means of mapping out large-scale geometric relationships as wave motions. Each of the eight “phase positions” represents a different element, and this is shown in the next figure:
Figure 4.4 – The eight “phase positions” as they relate to basic crystal structures formed by the elements.
So, to continue:
The easiest way to visualize such a “gateway” opening would be if you cut out a hole in a piece of cardboard, and then turned on a hair dryer and held the nozzle flat against the cardboard, then sliding it towards the hole. Until the nozzle actually reached the hole, the air has nowhere to go, and the engine will quickly run hard and overheat; but once the nozzle reaches the hole, the air has somewhere to go and the pressure is released, with the engine then relaxing. Inside the atom, via the Biefield-Brown effect, the pressure in the electron clouds is always trying to rush towards the nucleus, and unless the counter-rotating geometries connect, that pressure is blocked. In this sense, the lines and nodes in the geometric forms could be seen as the “holes” that are “popped” in the nested spherical fields, which will allow the in-streaming pressure to flow through.
Until the greatest number of “holes” have lined up between both geometries at the octave point of geometric balance, the full amount of outside pressure cannot flow towards the center. So, when the two forms “lock” together in valence periods that are not at the “octave” point, the counter-rotation of A1 and A2 is not fully balanced, causing additional pressure and lack of symmetry. A1 and A2 will then remain “stuck” in that unbalanced position if they are undisturbed by outside energy.
Thus, atoms and molecules that are not in such a state of balance are considered as “unstable” and will easily bond with other unstable atoms and molecules that hold the missing energy, in order to create equilibrium.
All elements are simply different proportional mixtures of A1 and A2, the nested tetrahedron and octahedron locked in different positions relative to each other, in Johnson’s model. The simplest example of this is that a single oxygen atom will naturally be attracted to two single hydrogen atoms to mutually blend into a water molecule, or H2O. Not surprisingly, the water molecule is shaped in the form of a tetrahedron. In later chapters on biology we will see the interesting possibilities that arise as a result of this unique structure.
The simplest example would be with sodium chloride or salt, which can be written as Na+Cl-, and forms either a cube or octahedron. The pressure difference between the positive and negative ions is what attracts them together in this case. The chlorine atoms are 1.81 angstroms wide in the salt molecule, almost twice as large as the sodium atoms at 0.97 angstroms.
The most basic example of this is a molecule of oxygen gas, written as O2. The only way that early (al)chemists were able to find these core elements such as the single oxygen atom were by disrupting basic chemical compounds through processes such as burning, freezing, mixing with acids and bases, et cetera.
However, any astute reader will have already seen that eight basic geometric positions are clearly not enough to form the entire Periodic Table; there must be some additional properties at work in order to produce the complete set of natural elements.
Figure 4.5 – Frequency contraction of tetrahedron (L) into octahedron (R).
Here is the key:
As seen in Figure 4.5, contracting a geometric shape is as simple as bisecting each of its lines into two or more equal-sized lengths and then connecting the dots together. When we divide each line into two pieces, this is called a “second-frequency” division, whereas dividing each line into three pieces would be called a “third-frequency” division. Starting with the tetrahedron, Buckminster Fuller demonstrated that a total of ten different frequencies (geometric shapes) could be created by this process of frequency expansion or contraction – and this is a central aspect of Johnson’s findings. For example, the “strong” force in the atomic nucleus is known to be exactly ten times more powerful than the “weak” force in the electron clouds! (This is usually written as the square root of 100, which is 10.) No other plausible explanation for this anomaly has ever been advanced. Here, the nucleus represents the point of the greatest “infolded” geometry at the highest frequency level of contraction.
Most interestingly, Carter’s “circlons” are spherical torus formations! Carter didn’t appear to know what the spiraling, curly, cyclical “rotations within rotations” were that he was diagramming between the circlons to show the various elements, simply that they had to exist by “absolute motion.” For a more complete description we invite the reader to peruse our detailed interview article and / or his website. In order to keep our thoughts simple for the purpose of this book, we will now simply point out some of the most obvious signs from quantum physics that Platonic geometries are indeed at work.
However, before the year 1900, light and heat were not thought to move in discrete “photon” units, but rather in a smooth, flowing, unbroken fashion. Physicist Max Planck was the first to discover that light and heat would move in “pulses” or “packets” of energy at the tiniest level, calculated to be about 10-32 centimeters. (An atomic nucleus is actually the size of a planet in comparison!) Interestingly, if you have a faster oscillation, you get bigger packets, and if you have a smaller oscillation you get smaller packets. Planck discovered that this relationship between the speed of oscillation and the size of the packet will always remain constant, regardless of how you measure it. This constant relationship between oscillation speed and packet size is known as Wein’s Displacement Law. Rigorously, Planck discovered a single number that expressed this relationship, which is now known as “Planck’s Constant.”
We can already see the answer to Hartmann’s question emerging in this book. As we had said, Planck’s discoveries came about through the study of heat radiation. The introductory paragraph to Caroline Hartmann’s article is a perfect description of what he accomplished:
Hartmann continues a bit later on:
The core of Planck’s work can be stated in a simple equation, which describes how radiating matter releases energy in “packets” or bursts. The equation is E=hv, where E equals the energy that you end up measuring, v is the vibrating frequency of the radiation that releases the energy, and h is what is known as “Planck’s Constant,” which regulates the “flow” between v and E.
This system is named after its founder, Rene Descartes, and all it means is that cubes are used to measure three-dimensional space. This is so commonly done that most scientists don’t even consider it as anything unusual – just length, width and height in action. In experiments such as Planck’s, a small cube was used to measure the energy that moved through that area of space. This cube was naturally assigned a volume of “one” (1) in Planck’s measuring system, for the sake of simplicity. However, when Planck wrote his constant he didn’t want it to be a decimal number, so he shifted the volume of the cube to 10. This made the constant 6.626 instead of 0.6626. What was truly important was the relationship between whatever was inside of the cube (6.626) and the cube itself (10.) Ultimately it did not matter whether you assigned the cube a value of one, ten or any other number, as the ratio would stay the same. Planck only discerned the constant nature of this ratio through rigorous experimentation over many years of time, as we said.
So then we must ask, “What is so important about 2/3rds?”
Figure 4.6 – Two tetrahedrons joined at a common face to form the “photon” measured by Planck’s constant.
Based on simple, measurable geometric principles explained by Fuller and others, we know that when we fit a tetrahedron perfectly inside of a sphere, it will fill exactly one-third of its total volume. The photon is actually composed of two tetrahedrons that are joined together, as we see in figure 4.6, and they then pass together through a cube that is only big enough to measure one of them at a time. The total amount of volume (energy) that moved through the cube will be two thirds (6.666) of the cube’s total volume, to which Planck had assigned the number 10. Buckminster Fuller was the first to discover that the photon was indeed composed of two tetrahedrons joined in this way, and he announced it to the world at his Planet Planning address in 1969, after which time it was obviously forgotten.
To put it in simpler terms, the aetheric energy of the “physical vacuum” will absorb a small amount of whatever energy passes through it. This means that it will “permit” slightly less energy to pass through it than what was originally released. So, once we factor in Coulomb’s equation, the numbers work perfectly. Furthermore, if we measure space using tetrahedral coordinates instead of cubical coordinates, then the need for Planck’s equation E=hv is removed, because the energy will now be measured to be the same on both sides of the equation – thus E (energy) will equal v (frequency) with no need for a “constant” between them.
We normally think of “photons” as carriers of light, but that is only one of their functions. More importantly, when atoms absorb or release energy, the energy is transmitted in the form of “photons.” Researchers such as Dr. Milo Wolff remind us that the only thing we know for certain about the term “photon” is that it is an impulse that travels through the aether/zero-point energy field. Now, we can see that this information has a geometric component, which suggests that the atoms must have such geometry as well.
In this case, two photons are released in opposite directions. Each photon is emitted from a separate atomic state that has been excited. Both atomic states are composed of identical atoms, and both are also decaying at the same rate. This allows two “paired” photons with the same energy qualities to be released in opposite directions at the exact same time. Both photons are then passed through polarization filters such as mirrors, which should theoretically change their direction of travel. If you have one mirror at a 45-degree angle, then you would naturally expect the photon to make a different angular turn than another photon would make if it was reflected off of a mirror at a 30-degree angle.
Clearly, within the framework of science, this is a perplexing phenomenon.
The photons will continue to maintain the same angular phase position relative to each other as the geometry that is between them expands.
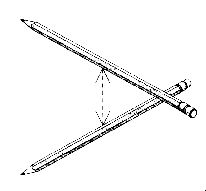
To visualize what is going on here, Johnson asks us to take two pencils of equal length and hold them perpendicularly to each other, also using the basic length of the pencil for the distance that separates them:
Figure 4.7 – Two pencils at 90-degree angles from each other, held equidistantly apart.
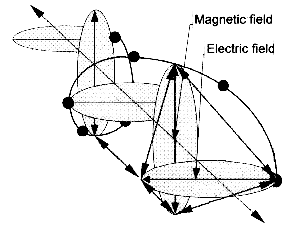
Now we can connect each tip of the top pencil to each tip on the bottom pencil. When we do this, we will form a four-sided object made of equilateral triangles between the two pencils – we will have a tetrahedron. We can work the same process with the electromagnetic wave, by having the total height of the electrostatic or magnetic wave (which both have the same height or amplitude) as our basic length, which was shown in figure 4.7 as pencils. Here in figure 4.8, we can see how the electromagnetic wave is actually tracing itself over a “hidden” (potential) tetrahedron when we connect the lines together using this same process:
Figure 4.8 – The hidden tetrahedral relationship in the electromagnetic wave.
It is important to mention here that this mystery has been continually discovered by various thinkers, only to be forgotten to science once more. The work of Lt. Col. Tom Bearden has rigorously shown that James Clerk Maxwell knew it was there when he wrote his complex “quaternion” equations, but Oliver Heaviside later distorted the model down to four simple quaternions and ruined the hidden tetrahedral “potential” inside. This hidden tetrahedron was also seen by Walter Russell, and later by Buckminster Fuller. Johnson was not aware of any of these previous breakthroughs when he first discovered it himself.
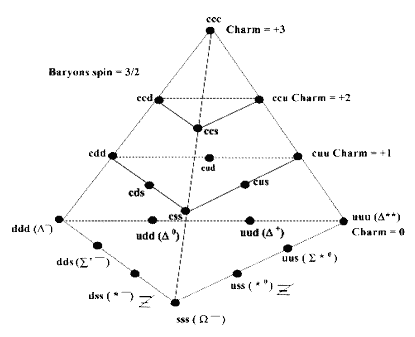
When an atomic structure was suddenly shattered, brief tracks would emerge that would fly away from the normal spiraling “particle” path in a bubble chamber, and they were named “quarks.” These “quarks” would disappear very quickly after they were first released. The geometry of their movements was carefully analyzed, since the only thing you can truly detect in a vapor-trail analysis is different geometric forms of movement. Many different forms of “quarks” were discovered, each with different geometric properties, misleadingly called such things as “color,” “charm” and “strangeness.” Murray Gell-Mann was the first to discover a unified model that showed how all these different geometric properties were interrelated, and he called it the “Eightfold Way.” Remarkably, the unified geometric structure that we see is a tetrahedron:
Figure 4.9 – The tetrahedron as seen in Gell-Mann’s “Eightfold Way” organization of “quarks.”
So what exactly are we seeing here? Each dot is obviously a different “quark.” Johnson tells us that “quarks” are released when the aetheric energy flow of the tetrahedron inside the atom is suddenly shattered. For a brief moment of time, the shattered energy fragments that are released will continue to flow with the same rotational / geometric properties as they had when they were bound in the atom, but they will very quickly dissolve back into the aether afterwards. One wouldn’t necessarily see all of the different “quarks” just by shattering one atom, since the angle at which the atom is shattered determines what part of its inner geometric Unity will be released. This is why the quarks had to be painstakingly studied separately. Even more interestingly, other “infolded” geometric frequencies such as the cuboctahedron are in Gell-Mann’s model as well; this tetrahedron is just one of three different hierarchies that he discovered.
In this next excerpt, Dr. Milo Wolff alludes to the fact that the geometry might be the solution to understanding the structure of the “nuclear space resonances” in the quantum realm, from page 198 of his book:
Interestingly, just as we were finishing this portion of the book, we were contacted by Dr. R.B. Duncan, who has a quite detailed and meticulous work published online that explains the structure of the atom based on the geometry of group theory that Wolff was mentioning above. Duncan had worked on this problem for thirty years of his life before publishing a solution!
Figure 4.10 – 180-degree spin angles of “electrons” caused by impulses moving over octahedral energy forms.
The next piece of evidence that we need to consider is spin. Physicists have known for many years now that energy particles “spin” as they travel. For example, “electrons” appear to be continually making sharp 180-degree turns or “half spins” as they move through the atom. “Quarks” are often seen to make “one thirds” and “two thirds” spins when they travel, which allowed Gell-Mann to organize their movements into the tetrahedron and other geometries. No one in the mainstream has provided a truly adequate explanation for why this is happening.
The tetrahedron must make either 120-degree (1/3 spin) or 240-degree (2/3 spin) rotations in order to have the same position. This will be explained more simply in section 4.9 just below here. (Other aether theorists such as Wolff, Crane, Ginzburg and Krasnoholovets have their own fluid-flow-based explanations for the phenomenon of half-spin.)
Thus, the spiraling movement of the torsion wave is caused by the simple geometry that it must pass through as it travels.
THE FINE-STRUCTURE CONSTANT
The fine structure constant is another aspect of quantum physics that few mainstream people have ever even heard of, probably since it is a totally unexplained embarrassment to the scientific mainstream that clings to particle-based models.
The electron cloud will always be “bumped” in a fixed, exact proportional relationship to the size of the photon. This means that if you have larger photons you will get larger “bumps” on the electron cloud, and smaller photons create smaller “bumps” on the electron cloud. This relationship remains constant, regardless of size. The fine-structure constant is another “dimensionless” number like Planck’s constant, meaning that we will get the same proportion regardless of how we measure it.
(We should again remember here that the word “coupling” simply means the joining together or separation of a photon and an electron:)
In Johnson’s model, the problem of the fine-structure constant has a very simple, academic solution. As we said, the photon travels along as two tetrahedrons that are paired together, and the electrostatic force inside the atom is maintained by the octahedron. By simply comparing the volumes between the tetrahedron and octahedron when they collide, we get the fine structure constant. All we do is divide the tetrahedron’s volume when it is surrounded (circumscribed) by a sphere into the octahedron’s volume when it is surrounded by a sphere, and we will get the fine-structure constant as the difference between them. In order to show how this is done, some additional explanation is required.
Therefore, you only need to rotate the tetrahedron by 120 degrees in order to bring it back into balance with the matrix of geometry that surrounds it, so that it is in the same position as it was before. This is easy to see if you visualize a car with triangular wheels, and you wanted to move it forward just enough that the wheels would look the same again. Each of the triangular wheels would have to turn 120 degrees to do this.
This next quote from Johnson explains the fine-structure constant based on this information:
A “radian volume” simply means that you calculate the volume of an object from its radius, which is half of the width of the object. (For those who wish to test the math out themselves, simply take the sine of 180 degrees and divide it by the sine of 120 degrees, then run that number through Coulomb’s equation to account for the slight loss of energy that happens when a pulsation is moving through the aether.) When this simple process of dividing the two “radian volumes” into each other is performed, the fine-structure constant will be the result.
These expanding or collapsing changes between the two objects are known as “tiling,” and Iuliano’s calculations were not very difficult to perform; it was simply that no one had thought to try it before. In Iuliano’s calculations, the volume of the two objects does not change; both the cube and the sphere have a volume that he set at 8pi times pi squared. When we tile them into each other, the only difference between the cube and sphere is in the amount of surface area. The extra surface area between the two is precisely equal to the fine-structure constant.
This is another aspect of the magic of “symmetry” in action, where we see that different geometric forms can have similar properties, since they all nest inside of each other with perfect harmonic relationships. Both Johnson and Iuliano’s perspectives show us that we are dealing with a geometrically structured aetheric energy at work in the atom.
This has long been a central element in the esoteric traditions of “sacred geometry,” as it was believed to show the balance between the physical world, represented by the square or cube, and the spiritual world, represented by the circle or sphere. Now we can see that this was yet another example of “hidden knowledge” that was encoded in a metaphor, so that eventually people in our time would regain the true understanding of the secret science behind it. They knew that once we discovered the fine-structure constant, we probably would not understand what we had observed, so this ancient knowledge was left behind to show us the key.
Our presentation of Johnson’s physics has been designed to be as simplified and streamlined as possible, so anyone who would attempt to challenge the model scientifically would be required to read more about it in order to truly grasp its many nuances. Yet, for those who have an open mind, the data that we have presented here is more than enough to prove the point. The key is that sacred geometry has always existed in the quantum realm; it just remained undiscovered amongst the various anomalies of quantum physics that had remained unexplained until this time, as the mainstream continues to be shackled to outmoded “particle” models.
We remember that pieces of wreckage from the Roswell Crash were said to be unbelievably lightweight, yet they were so strong that they could not be cut, burned or damaged in any way. This is the type of material that we will be able to build once we fully understand the new quantum physics.
The geometry is so compact and precise inside that there is literally no “room” for a current to move through the molecules.
Much of this material is a review from previous volumes, but it is nevertheless important that we cover it once more. After we establish this crucial link between the geometry of the quantum and the geometry of the macro, effectively proving the existence and importance of these new theories, we will move on to delineate an entirely new model of the Cosmos that is based on all of the principles that we have discussed up until this point.
|
Monday, November 3, 2008
The Sequenttail Perspective
Subscribe to:
Post Comments (Atom)
Copy and paste picture link
No comments:
Post a Comment