SACRED GEOMETRY IN THE QUANTUM REALM

by David Wilcock 2002 from NoNeedToKnow Website ATLANTEAN SECRETS REVISITED As illustrated in our previous volume, a majority of the unified cosmological picture that we have been describing in this book is provided in exquisite detail throughout the Vedic scriptures, which date themselves as being 18,000 years old. It is highly likely that the entire cosmology that we are discussing was well known by both the Atlanteans and the Ramans during ancient times. Then, roughly 12,000 years ago, a worldwide cataclysm caused the destruction of both civilizations. As the years passed, those who inherited the scientific knowledge would have more and more difficulty seeing “the big picture.” Almost all sacred traditions, including those of the Vedas, insisted that there was a hidden order that unified all aspects of the Universe, and that with sufficient study and visualization of the underlying geometric forms of this order, the mind of the Initiate could be connected with the Oneness of the Universe, enabling great feats of consciousness and mind-over-matter capability to occur. Some of these visualizations took the form of studying mandalas, such as the Sri Yantra formation. Others preferred to engage in dances where the movements and music were in tune with these geometric patterns. Still others preferred to assemble, sculpt and / or draw these forms with a compass and straightedge, hence the importance of the main symbol of the Masonic fraternity, which has the letter “G”, symbolizing “God,” “Geometry” and the “Great Architect of the Universe,” surrounded by a compass above it and a straightedge below it. Pre-Masonic groups such as the Knight Templars chose to encode these geometric relationships into their sacred structures, such as the stained-glass windows in cathedrals. SACRED GEOMETRY AND THE PLATONIC SOLIDS Hence, the cornerstone of knowledge for secret mystery schools regarding this hidden order in the Universe has always been sacred geometry. We have written extensively on this subject in both of our previous books, and the reader is encouraged to refer back to them for greater understanding. In short, sacred geometry is simply another form of vibration, or “crystallized music.” Consider the following example: First, we vibrate a guitar string. This creates “standing waves,” meaning waves that do not move back and forth across the string but remain stable in one place. We will see some areas where there is an extreme of vertical movement, representing the top and bottom of the wave, and other areas where there is no vertical movement, known as nodes. The nodes that are formed in any type of standing wave will always be spaced evenly apart from each other, and the speed of the vibration will determine how many nodes will appear. This means that the higher the vibration rises, the more nodes we will see. In two dimensions, we can either use an oscilloscope or vibrate a flat circular “Chladni plate” and see nodes develop that will form common geometric forms such as the square, triangle and hexagon when connected together. This work has been repeated many times by Dr. Hans Jenny, Gerald Hawkins and others. - If the circle has three equally spaced nodes, then they can connect to form a triangle - If the circle has four equally spaced nodes, it can form a square - If it has five nodes, it forms a pentagon - Six nodes form a hexagon, et cetera Though this is a very simple concept in terms of wave mechanics, Gerald Hawkins was the first to establish mathematically that such geometries inscribed within circles were indeed musical relationships. We may be surprised to realize that he was led to this discovery by analyzing various geometric crop formations that would appear overnight in the fields of the British countryside. This has been covered in both of our previous volumes. The deepest, most revered forms of sacred geometry are three-dimensional, and are known as the Platonic solids. There are only five formations in existence that follow all the needed rules to qualify, and these are the eight-sided octahedron, four-sided tetrahedron, six-sided cube, twelve-sided dodecahedron and twenty-sided icosahedron. Here, the tetrahedron is shown as a “star tetrahedron” or interlaced tetrahedron, meaning that you have two tetrahedra that are joined together in perfect symmetry: Figure 3.1 – The five basic Platonic Solids. Here are some of the main rules for these geometric solids: - Each formation will have the same shape on every side: equilateral triangle faces on the octahedron, tetrahedron and icosahedron square faces on the cube pentagonal faces on the dodecahedron - Every line on each of the formations will be exactly the same length. - Every internal angle on each of the formations will also be the same. And most importantly, - Each shape will fit perfectly inside of a sphere, all the points touching the edges of the sphere with no overlaps. Similar to the two-dimensional cases involving the triangle, square, pentagon and hexagon inside the circle, the Platonic Solids are simply representations of waveforms in three dimensions. This point cannot be stressed strongly enough. Each tip or vertex of the Platonic Solids touches the surface of a sphere in an area where the vibrations have canceled out to form a node. Thus, what we are seeing is a three-dimensional geometric image of vibration / pulsation. Both the students of Buckminster Fuller and his protégé Dr. Hans Jenny devised clever experiments that showed how the Platonic Solids would form within a vibrating / pulsating sphere. In the experiment conducted by Fuller’s students, a spherical balloon was dipped in dye and pulsed with “pure” sound frequencies, known as the “Diatonic” sound ratios. A small number of evenly-distanced nodes would form across the surface of the sphere, as well as thin lines that connected them to each other. If you have four evenly spaced nodes, you will see a tetrahedron. Six evenly spaced nodes form an octahedron. Eight evenly spaced nodes form a cube. Twenty evenly spaced nodes form the dodecahedron, and twelve evenly spaced nodes form the icosahedron. The straight lines that we see on these geometric objects simply represent the stresses that are created by the “closest distance between two points” for each of the nodes as they distribute themselves across the entire surface of the sphere. Figure 3.2 – Dr. Hans Jenny’s Platonic Solid formation in spherical vibrating fluid. Dr. Hans Jenny conducted a similar experiment, a small part of which is pictured here in Figure 3.2, wherein a droplet of water contained a very fine suspension of light-colored particles, known as a “colloidal suspension.” When this roughly spherical droplet of particle-filled water was vibrated at various “Diatonic” musical frequencies, the Platonic Solids would appear inside, surrounded by elliptical curving lines that would connect their nodes together, as we see in the picture, where it is clear that there are two tetrahedrons in the central area. If the droplet were a perfect sphere instead of a flattened sphere, then the formations would be even more clearly visible. PLATONIC SOLIDS AND “SYMMETRY” IN PHYSICS The mystery and significance of the Platonic Solids has not been completely lost to modern science, as these forms fit all the necessary criteria for creating “symmetry” in physics in many different ways. For this reason, they are often seen in theories that deal with multi-dimensionality, where many “planes” need to intersect in symmetrical ways so that they can be rotated in a number of ways and always remain in the same positions relative to each other. These multi-dimensional theories include “group theory,” also known as “gauge theory,” which consistently features various Platonic models for “infolded” hyperdimensional space. These same “modular functions” are considered to be the most advanced mathematical tools available for the study and understanding of “higher dimensions,” and the “Superstring” theory is entirely built off of them. In short, the Platonic Solids are already known to be the master key to unlock the world of “higher dimensions.” Remember that we have only briefly mentioned the above points, as they have been well-addressed in our previous volumes, and the key is symmetry. When we keep in mind the symmetrical quality of the Solids as we have indicated, Dr. Wolff’s words from Chapter 5 entitled On the Importance of Living in Three Dimensions should make good sense to us: Pg. 71 – As your advisor in exploration, I can tell you, “Whenever you see a situation of symmetry in a physical problem, stop and think! Because you will nearly always find an easier way to solve the problem by using the symmetry property.” This is one of the rewards of playing around with symmetry. The ideas are neat… In mathematics and geometry, there is a need to be precise; so there symmetry is defined to mean that a function or a geometric figure remains the same, despite: 1) a rotation of coordinates, 2) movement along an axis, or 3) an interchange of variables. In physical science, which is our main concern, the existence of a symmetry usually means that a law of Nature does not change, despite: 1) a rotation of coordinates in space, 2) movement along an axis through space, 3) changing the past into the future such that t becomes –t, 4) an interchange of two coordinates such as exchanging x with y, z with –z, etc. or, 5) the change of any given variable. [emphasis added] The Platonic Solids have the greatest geometric symmetry of any shapes in existence, though Dr. Wolff does not call them by name here. In the next excerpt from Dr. Aspden, he refers to the Platonic Solid forms in the aether as “fluid crystals,” and explains how they can have an effect similar to a solid, even while they are appearing in a fluidlike medium: …19th century physicists were puzzled by the aether because it exhibits some properties telling us it is a fluid and some telling us it is a solid. That was the perception from a time when little if anything was known about ‘fluid crystals’. The displays in many pocket calculators use electrical signals and rely on the properties of a substance that, like the aether, exhibits properties characteristic of both the liquid state and the solid state as a function of electric field disturbances. [emphasis added] This gives us a “solid” explanation for why Tesla said that the aether “behaves as a liquid for matter, and as a solid for light and heat". The Platonic Solids actually do act as if they were structural frameworks within the aether, organizing the energy flows into specific patterns. Hence, the Platonic Solids are the simple geometric forms of “crystallized music” that will naturally form themselves in the aether when it pulsates. Another important point to remember is that as the hierarchy of Platonic Solids “grow” into each other, the movement will always occur along spiral pathways, predominantly rooted in the classic “phi” ratio. Torsion waves have been seen to follow the “phi” pattern as well, which shall be more fully explored when we discuss the under-appreciated “pyramid power” phenomenon and the “cavity structural effect” pioneered by Dr. Victor Grebennikov in Chapter Seven. MICROCLUSTER PHYSICS Just as we were finishing up the first half of this book, a new associate alerted us to the burgeoning new field of “microcluster physics,” which changes our entire view of the quantum world by presenting us with a whole new phase of matter that does not obey the conventionally accepted “rules.” Microclusters are tiny “particles” that present clear and straightforward evidence that atoms are vortexes in the aether that naturally assemble into Platonic Solid formations by their vibration / pulsation. Furthermore, these new discoveries pose quite a challenge for those who still believe that there must be single electrons orbiting a nucleus instead of standing-wave electron clouds of aetheric energy that assemble into geometric patterns. The story of “microclusters” first broke into the mainstream world in the December 1989 issue of Scientific American, in an article by Michael A. Duncan and Dennis H. Rouvray: Divide and subdivide a solid and the traits of its solidity fade away one by one, like the features of the Cheshire Cat, to be replaced by characteristics that are not those of liquids or gases. They belong instead to a new phase of matter, the micro cluster… They pose questions that lie at the heart of solid-state physics and chemistry, and the related field of material science. How small must an aggregate of particles become before the character of the substance they once formed is lost? How might the atoms reconfigure if freed from the influence of the matter that surrounds them? If the substance is a metal, how small must this cluster of atoms be to avoid the characteristic sharing of free electrons that underlies conductivity? Less than two years after this story broke in the mainstream, the science of microcluster physics was realized in its own graduate-school textbook authored by Satoru Sugano and Hiroyasu Koizumi. Microcluster Physics was published by the respectable, mainstream Springer-Verlag corporation as volume 21 in a series of texts in the field of materials science. All of the quotes from this text that we shall use are from its revised second edition, which was released in 1998. In Sugano and Koizumi’s text, we are told that with the new discoveries of microclusters, we can now arrange groupings of atoms into four basic categories of size, each with different properties: - Molecules: 1-10 atoms - Microclusters: 10-1000 atoms - Fine Particles: 1000-100,000 atoms - Bulk: 100,000+ atoms When we study the above list, we would initially expect that microclusters would have traits in common with molecules and with fine particles both, but in fact they have properties that neither display, as Sugano et al. explain here: Microclusters consisting of 10 to 10^3 atoms exhibit neither the properties of the corresponding bulk nor those of the corresponding molecule of a few atoms. The microclusters may be considered to form a new phase of materials lying between macroscopic solids and microscopic particles such as atoms and molecules, showing both macroscopic and microscopic features. However, research into such a new phase has been left untouched until recent years by the development of the quantum theory of matter. As we continue reading, we learn that microclusters do not form randomly from any group of 10-1000 atoms; only certain “magic numbers” of atoms will gather together to form microclusters. The next quote describes how this was first discovered, and when we read it we should remember that the “mass spectrum” being mentioned describes spectroscope analysis, which we covered in the last chapter. When “cluster beams” are being discussed, this means that atoms (such as Na, or sodium) are being blasted through a tiny nozzle to form into a “beam” that is then analyzed. Most importantly, as the atoms blast out of the nozzle, some of them spontaneously gather into microclusters, which demonstrate anomalous properties: The microscopic features of microclusters were first revealed by observing anomalies of the mass spectrum of a Na [sodium] cluster beam at specific sizes, called magic numbers. Then it was experimentally confirmed that the magic numbers come from the shell structure of valence electrons. Being stimulated by these epoch-making findings in metal microclusters and aided by progress of the experimental techniques producing relatively dense, non-interacting microclusters of various sizes in the form of microcluster beams, the research field of microclusters has developed rapidly in these 5 to 7 years [since the first 1991 edition of the book.] The progress is also due to the improvement of computers and computational techniques… The field of microclusters is attracting the attention of many physicists and chemists (and even biologists!) working in both pure and applied research, as it is interesting not only from the fundamental point of view but also from the viewpoint of applications in electronics, catalysis, ion engineering, carbon-chemical engineering, photography and so on. At this stage of development, it is felt that an introductory book is required for beginners in this field, clarifying fundamental physical concepts important for the study of microclusters. This book is designed to satisfy such a requirement. It is based on series of lectures given to graduate students (mainly in physics) of the University of Tokyo, Kyoto University, Tokyo Metropolitan University, Tokyo Institute of Technology and Kyushu University in the period of 1987-1990. Our next quote comes from the first area in Sugano and Koizumi’s book where specific details are given regarding the highly anomalous physical properties of microclusters. Though they are only slightly smaller than fine particles in terms of the number of atoms, they are much more stable. Here, the greater stability refers to the fact that microclusters burn at a much higher temperature than molecules or fine particles of the same elements. According to David Hudson, (whom we shall discuss later,) Russian scientists were the first to discover that microclusters must be burned for more than 200 seconds to reveal a color spectrum to be analyzed, whereas all other known molecular compounds burn up in a maximum of about 70 seconds: When we arrive at the fragment called microcluster with a radius of the order of 10 angstroms by further dividing fine particles, we see that we have to use physics different from that for fine particles. The essential difference is derived from the theoretical postulate, partly supported by experiments, that microclusters of a given shape and size can, in principle, be extracted and their properties can be measured, even though this kind of measurement is impossible for fine particles. This postulate may be justified by considering the fact that clusters of a given regular shape are very stable as compared with those of the other shapes, the number of which is rather small. In contrast to this fact, fine particles of different shapes and a fixed size forming a big ensemble to allow a statistical treatment are nearly degenerate in energy. This makes impossible the extraction of fine particles of a given shape. Clear-cut evidence has been obtained such that microclusters of alkali [1.8] and noble [1.9] metal elements in the form of a cluster beam have a nearly spherical shape at the size of the so-called magic numbers. A magic number means a specific size N [i.e. the number of atoms in the cluster] where anomalies of abundance in the mass spectra are found. This indicates that microclusters of those sizes are relatively stable as compared with those of neighboring sizes. The “nearly spherical” shapes that are described above will be seen in later quotes as the Platonic Solids and related geometries. Our next passage is probably too technical for most readers and can be skipped over, but it is a clear-cut description of how the “cluster beams” are being made and analyzed and what specific “magic numbers” of atoms emerged. Furthermore, we should note that the clusters that are formed become electrically neutral, which is another anomalous and unexpected result: As an example, we show the mass spectrum of the Na cluster beam in Fig. 1.5. The beam is produced by the adiabatic expansion of a heated Na and Ar gas mixture through a nozzle. The Na clusters in the beam are photoionized, mass analyzed by a quadrupole mass analyzer, and finally detected by an ion-detection system. Detailed examinations of the experiment verify that the mass spectrum thus observed reflects that of [electrically] neutral clusters originally produced by the jet expansion. The anomalies of abundance of the size N, being 8, 20, 40, 58 and 93 (Fig. 1.5), are regarded as the magic numbers of neutral Na clusters. Now pay very close attention to the next sentence, as its significance can easily be missed: In what follows, we shall show that these magic numbers are associated with the shell structure of valence electrons moving independently in a spherically symmetric effective potential… What this is telling us is that the hypothetical “electrons” are no longer bound to their individual atoms in microclusters, but rather move independently throughout the entire cluster itself! Remember that in our new quantum model, there are no electrons, only clouds of aetheric energy that are flowing in towards the nucleus via the Biefield-Brown effect. In this case, the microcluster acts as one single atom, with the center of the cluster becoming akin to the positively-charged atomic nucleus where the negatively-charged energy is flowing in. Interestingly, in keeping with the fluidlike behaviors of the aether, the next passage suggests that the microclusters can have properties similar to a fluid as well as a solid: [The symmetry of] metal microclusters seems to reveal that microclusters belong to the microscopic world like atoms and molecules, whereas fine particles belong to the macroscopic world. This is true in some aspects, but not so in every aspect. In Chap. 2 we shall discuss that, at finite internal temperatures, microclusters may reveal the liquid phase as encountered in the macroscopic world... The next excerpt comes from a completely different study by Besley et al., referenced at the end of this chapter, entitled Theoretical Study of the Structures and Stabilities of Iron Clusters. Obviously, their work builds directly off of Sugano and Koizumi’s textbook and the findings that went into its production. Here, the key is that Besley et al.’s research points to anomalous electrical and magnetic properties possessed by microclusters that are not seen either in molecules or in condensed matter: Clusters are also of interest in their own right, since for small clusters there is the possibility of finite size effects leading to electronic, magnetic or other properties which are quite different from those of molecules or condensed matter. There has also been a considerable research effort into understanding the geometries, stabilities and reactivities of gas phase bare metal clusters from a theoretical viewpoint. And now, as we skip ahead to page 11 of Sugano et al.’s microcluster physics textbook, we come to section 1.3.1 entitled Fundamental Polyhedra. This is where the connection between microclusters and the geometry of Johnson’s physics becomes readily apparent: Recently, it has been discussed [1.12] that stable shapes of microclusters are given by Plato’s five polyhedra; the tetrahedron, cube, octahedron, pentagonal dodecahedron, icosahedron, [i.e., the Platonic Solids]; and Keplers’ two polyhedra of rhombic faces; the rhombic dodecahedron and rhombic triacontahedron… It is very important to note that tetrahedra are not space-filling, as shown in Fig. 1.9, and icosahedra, trigonal decahedra and pentagonal dodecahedra with five-fold rotational symmetry are non-crystalline structures: they do not grow into the periodic structure of the bulk. If the polyhedron is a non-crystalline structure, then the microcluster has to undergo a phase transition to a crystalline structure on the way of growing into the bulk. For one who has studied sacred geometry for many years, it is amazing to consider that at a level far too tiny for the naked eye, atoms are grouping together into perfect Platonic Solid formations. It is also interesting to consider that some of these microclusters also have fluidlike qualities, allowing them to flow from one type of geometric structure into another. In their text, Sugano and Koizumi have assumed that certain polyhedra such as the icosahedron and dodecahedron are non-crystalline, and must therefore undergo a phase change before they could become a larger crystallized object. However, later in this chapter we will present hard, irrefutable evidence that the entire model of crystallography is flawed, and that under certain circumstances, formations very similar to microclusters can be formed at larger levels of size, from two or more atomic elements grouped together. Importantly, as the reader thumbs through the rest of Sugano et al.’s textbook, scores of diagrams of atoms grouped into Platonic Solids are seen. We learn that the “magic number” groupings of atoms will, in every case, form into one of the geometric structures mentioned above. If we took a tetrahedron, for example, and constructed it out of a certain number of marbles that all had an equal width, then we would need an exact “magic” number of marbles to construct a tetrahedron of a given size. This is the same as Buckminster Fuller’s model of “close-packed spheres,” and in its simplest form is expressed by seeing that if you put three marbles together into a triangle and then place a fourth marble above it in the middle, you will see a tetrahedron form. Even more interestingly, on page 18 of the Microcluster Physics textbook, Sugano et al. have a photograph of a gold cluster consisting of “about 460” atoms, where we can clearly see the close-packed sphere structure of the atoms inside, forming unmistakable geometry. These images are taken by a scanning electron microscope at very high magnification, and the structure of the cuboctahedron geometry [Fig. 3.3, L] is clearly visible in a series of different angles. Interestingly, the cluster is seen to undergo different geometric changes from the cuboctahedron to other forms in its structure from image to image, again suggesting a fluidlike quality, and unseen “stresses” in the aether at work. Figure 3.3 is an artist-rendered diagram of how the “magic number” of 459 spherical atoms will pack together to form a cuboctahedron-shaped cluster, whereas 561 atoms will cluster into the form of an icosahedron. Figure 3.3 - Cuboctahedral cluster of 459 atoms (L) and Icosahedral cluster of 561 atoms (R) Our next quote comes from section 3 of Besley et al.’s study, which discusses the “jellium” model and makes it very clear that the individual nature of the atoms in a microcluster is lost in favor of a group behavior. Again we will see the mentioning of magic numbers and of electrons moving through the entire structure instead of just through their parent atom; we also see the hypothesis that “geometric shells” of electrons are somehow formed in the microcluster. For small clusters of simple metals, such as the alkali metals, mass spectroscopic studies have indicated the presence of preferred nuclearities or “magic numbers” corresponding to particularly intense peaks. These experiments led to the development of the (spherical) jellium model, wherein the actual cluster geometry (i.e. the nuclear coordinates) are unknown and unimportant (perhaps because the clusters are molten or rapidly fluxional) and the cluster valence electrons are assumed to move in a spherically average central potential. The jellium model therefore explains cluster magic numbers in terms of the filling of cluster electronic shells, which are analogous to the electronic shells in atoms. For somewhat larger nuclearities (N ~ 100-1500 [total atoms in the cluster,]) there are periodic oscillations in mass spectral peak intensities which have been attributed to the bunching together of electronic shells into supershells. The observation of long period oscillations in the intensities of peaks in the mass spectra of very large metal clusters (with up to 10^5 atoms) has led to the conclusion that such clusters grow via the formation of 3-dimensional geometric shells of atoms and that for these nuclearities it is the filling of geometric rather than electronic shells that imparts extra cluster stability. Certainly, the idea of “supershells” of electrons suggests a fluidlike blending together of atoms in the quantum realm. Again, it appears that the entire idea of electrons is flawed, since the next passage from Besley et al., tells us that the “jellium” model where “particle” electrons fill up into “geometric shells” does not work for what are known as transition metals. Since there can be no individual electrons at this point, Besley et al. hypothesize the existence of “explicit angular-dependent many-body forces.” In short, a “fluid crystal” aetheric quantum model is essentially required to explain the forces that create microclusters: For transition metals there is no clear evidence that the jellium model holds, even for low nuclearities… we would hope that a model which introduces explicit angular-dependent many-body forces (as in the MM [Murrell-Mottram] model that we have adopted) will fare better at explaining cluster structure preferences. As we think through the results of these microcluster studies, we must not forget that the Platonic Solids are very easily formed by vibrating a spherical area of fluid. It is quite surprising that the microcluster researchers do not appear to have noticed this connection. The prevailing view of quantum mechanics as a particle phenomenon has such a strong hold on the minds of scientific researchers that elaborate explanations involving “geometric shells” of electrons must be invoked. The key question that must be addressed is how and why this geometry would form – and the idea of a vibrating, fluidlike quantum medium is by far the simplest answer. A microcluster is simply a larger “aetheric atom” in a perfect geometric form. DAVID HUDSON AND “ORMUS ELEMENTS” KNOWN ORMUS ELEMENTS Element Atomic Number Cobalt 27 Nickel 28 Copper 29 Ruthenium 44 Rhodium 45 Palladium 46 Silver 47 Osmium 76 Iridium 77 Platinum 78 Gold 79 Mercury 80 Table 3.1 – Known Metallic Microclusters or “Ormus” Elements in David Hudson’s patent. Next, we introduce the work of David Hudson, who discovered a substance that turned out to contain microclusters in a goldmine on his property in the late 1970s. He spent several million dollars having these mysterious materials analyzed and tested in various ways, and in 1989 Hudson patented his microcluster discovery by naming them Orbitally Rearranged Monatomic Elements, or “ORMEs.” [The name is usually changed to “Ormus” or “M-state” elements when discussed online so as not to interfere with Hudson’s copyrights.] Hudson displays a broad knowledge of microcluster physics in his published lectures from the early 1990s, but his findings are more controversial than what we find in Sugano et al.’s textbook or other published mainstream sources. Hudson’s patent focuses on the microcluster structures he found in the following precious metal elements. (We should note here that Sugano and Koizumi have established that microclusters have been found in non-metallic elements as well.) Hudson found that all of the above microcluster metals exist plentifully in sea water. Even more surprisingly, Hudson discovered that these elements in the microcluster state may be up to 10,000 times more abundant on Earth than in their common metallic state. Hudson’s research demonstrated that these metallic microclusters are found throughout many different biological systems, including many different plants, and that they form up to 5% of the material in a calf’s brain by weight. Furthermore, they act as room-temperature superconductors, have superfluid qualities and levitate in the presence of magnetic fields, since no magnetic energy is able to penetrate through their outer shells. Their physical qualities match the descriptions of various materials in alchemical traditions from China, India, Persia and Europe. Various people have volunteered to ingest gold microclusters or “monatomic gold,” and have reported experiencing the same psychic effects as the kundalini changes noted in the Vedic scriptures of ancient India. Even more controversial are Hudson’s patented discoveries surrounding the heating of iridium microclusters. As the material is heated, its weight is seen to increase by 300 percent or more. Even more surprisingly, as microcluster iridium is heated to 850 degrees Celsius, the material disappears from physical view and loses all of its weight. However, when the temperature is again reduced, the microcluster iridium will reappear and regain most of its former weight. In Hudson’s patent, he has a chart that was generated by thermo-gravimetric analysis that shows this effect in action. The idea of a material gaining weight, then spontaneously losing weight and disappearing from all physical view is no longer out of place when we combine Kozyrev’s findings with Ginzburg’s changes to conventional relativity equations and Mishin and Aspden’s discoveries of multiple densities of aether. In the first chapter, Kozyrev showed how the heating or cooling of an object can affect its weight in subtle but measurable ways. We also saw that these weight increases and decreases occur in sudden “quantized” bursts, not in a smooth, flowing fashion. Dr. Vladimir Ginzburg suggested that an object’s mass is converted into pure field as it approaches the speed of light, and Mishin and Aspden’s data suggests that the mass is actually moving into a higher density of aetheric energy. Thus, Hudson’s observed and patented effects with microcluster iridium provide the first major proof in this volume for the idea that an object can be completely displaced into a higher density of aetheric energy. In the case of microcluster iridium, it would seem that the geometric structure of the microcluster allows for heat energy to be harnessed much more efficiently. This harnessing of the vibrations of heat then creates extreme resonance at a lower relative temperature, bringing the internal vibrations of the iridium past the speed of light. (These internal vibrations may already be relatively close to the speed of light before such added resonance is introduced, due to the speed at which aether flows through the atomic “vortex” of negative electron clouds and the positive nucleus.) Then, when the threshold point of light-speed is finally reached, the aetheric energy of the iridium is displaced into a higher density, thus causing it to disappear from measurable view. When the temperature is reduced, the iridium again displaces back down into our own density, since the pressure that was holding it in the higher density has now been eliminated. ANOMALIES OF CRYSTAL FORMATION Now that we have covered the anomalous area of microclusters, we are ready to tackle the more conventionally understood problems of crystal formation. Common table salt is a perfect example of how two different elements, sodium and chloride, can bond together and form a Platonic Solid geometry, in this case the cube. Two hydrogen atoms and one oxygen atom form together in the shape of a tetrahedron to create the water molecule, (which is not a crystal in the liquid state but has a tetrahedral molecule,) and fluorite crystals form the octahedron. Crystals that form with these properties will maintain the same orientation throughout themselves, and are symmetrical. A more technical description is that crystals are, “solids which have flat surfaces (facets) that intersect at characteristic angles, and are ordered at a microscopic level.” Our key question to remember here would be, “Why do spherical energy vortexes end up joining together in these characteristic geometric angles and patterns?” The answer, of course, shall be found in our understanding of the Platonic Solids as “harmonic” energy structures in the aether. Glusker & Trueblood’s classical definition for how crystals are formed is that they are produced by: …a regularly repeating arrangement of atoms. Any crystal may be regarded as being built up by the continuing three-dimensional translational repetition of some basic structural pattern. [emphasis added] The term “translation” means that we rotate a specific object by an exact number of degrees, such as 180, which would form a “two-fold” crystal since there are two such translations in a 360-degree circle. Thus, “translational repetition” means that that the basic structural element (atom or molecular group of atoms) making up a crystal can be rotated again and again in the same way to form the repeated pattern. The technical term for such a regular arrangement of atoms is periodicity, which means that a crystal is made up of “some basic structural unit which repeats itself infinitely in all directions, filling up all of space” within itself. The same structure (atom or group of atoms) keeps repeating in the same, periodic way, hence the term periodicity. In this classical theory of “periodic” crystal formation, each atom retains its original size and shape and does not affect any of the other atoms except for those it is directly bonded to. It is important to realize that the model of periodicity worked very well in crystallography. Any type of crystal that had been discovered could be analyzed with this method, and the angles between all of the facets could be predicted based on simple geometric principles. Then in 1912, Max von Laue discovered a way to use X-rays to illuminate the inner structure of crystals, creating what is known as a “diffraction diagram.” The diagram appears as an arrangement of single points of light on a black background. This led to a whole science of X-ray crystallography that was formalized by William H. and William L. Bragg, where the points of light are analyzed geometrically in relation to each other in order to determine what the structure of the true crystal actually is. For seventy years after this technology was developed, every diffraction diagram that had ever been observed by mainstream scientists fit the periodicity model perfectly, which led to the inevitable and apparently quite simple conclusion that all crystals were an arrangement of single atoms as structural units. One of the periodicity model’s most straightforward mathematical rules is that a crystal can only have 2-, 3-, 4-, and 6-fold rotations (translations.) In this model, if you have a crystal that is indeed made of single atoms or molecules in a repeating, periodic structure, the crystal cannot have a five-fold rotation or any rotation higher than 6. Atoms are “supposed” to retain their own individual point-like identities and not merge with other atoms into a larger whole. Nevertheless, in terms of pure geometry, the dodecahedron has 5-fold symmetry and the icosahedron has 5- and 10-fold symmetry. These Platonic Solids fit all the requirements for symmetry as outlined by Dr. Wolff earlier in this chapter, but you simply cannot pack single atoms together to make either of these shapes. So again, the dodecahedron and icosahedron have symmetry, but they do not have periodicity as crystal formations. Therefore, there was no provision in science to believe that either of these forms would appear as a molecular, crystalline structure – it was “impossible.” Or so they thought… Now enter the infamous Roswell crash. According to former Groom Lake / Area 51 employee Edgar Fouche, molecular structures were found on the recovered hardware that did not fit the conventional model of crystalline periodicity. These became known as “quasi-crystals,” short for “quasi-periodic crystals.” Both the icosahedron and dodecahedron have appeared in these unique alloys. Similar to microclusters but on a larger level of size, these quasi-crystals were discovered to have many strange properties, such as extreme strength, extreme resistance to heat and being non-conductive to electricity, even if the metals involved in their creation would normally act as conductors! (This will be explained as we progress.) Unlike microclusters, which only appear to be able to be formed individually from “cluster beams”, quasi-crystals can be grouped together into usable alloys. Fouche states the following on his website, with our added emphasis: I’ve held positions within the USAF that required me to have Top Secret and ‘Q’ Clearances and Top Secret-Crypto access clearances… In the mess hall at [the top-secret] Groom [Lake facility,] I heard words like Lorentz Forces, pulse detonation, cyclotron radiation, quantum flux transduction field generators, quasi-crystal energy lens and EPR quantum receivers. I was told that quasi-crystals were the key to a whole new field of propulsion and communication technologies. To this day I’d be hard pressed to explain to you the unique electrical, optical and physical properties of quasi-crystals and why so much of the research is classified… Fourteen years of quasi-crystal research has established the existence of a wealth of stable and meta-stable quasi-crystals with five-, eight-, ten- and twelve-fold symmetry, with strange structures [such as the dodecahedron and icosahedron] and interesting properties. New tools had to be developed for the study and description of these extraordinary materials. I’ve discovered that the classified research has shown that quasi-crystals are promising candidates for high energy storage materials, metal matrix components, thermal barriers, exotic coatings, infrared sensors, high power laser applications and electro-magnetics. Some high strength alloys and surgical tools are already on the market. [Note: Wilcock was personally told in 1993 that Teflon and Kevlar are both reverse-engineered.] One of the stories I was told more than once was that one of the crystal pairs used in the propulsion of the Roswell crash was a Hydrogen Crystal. Until recently, creating a Hydrogen crystal was beyond the reach of our scientific capabilities. That has now changed. In one Top Secret Black Program, under the DOE, a method to produce hydrogen crystals was discovered, [and] then manufacturing began in 1994. The lattice of hydrogen quasi-crystals, and another material not named, formed the basis for the plasma shield propulsion of the Roswell craft and was an integral part of the bio-chemically engineered vehicle. A myriad of advanced crystallography undreamed of by scientists were discovered by the scientists and engineers who evaluated, analyzed and attempted to reverse engineer the technology presented with the Roswell vehicle and eight more vehicles which have crashed since then. Arguably after 35 years of secret research on the Roswell hardware, those who had recovered these technologies still had hundreds if not thousands of unanswered questions about what they had found, and it was deemed “safe” to quietly introduce “quasi-crystals” to the non-initiated scientific world. There are now literally thousands of different references to quasi-crystals on the Internet, completely separate from any mention of microclusters. (Not a single scientific study that we have been able to find online mentions both microclusters and quasi-crystals in the same document.) Many of the quasi-crystal references are from companies that are government contractors, and it is very easy to see that they are being studied with widespread intensity. However, they are almost never mentioned in the general media, even though they present such a unique challenge to our prevailing theories of quantum physics. The research goes on, but it is with a very subdued excitement. Dan Schechtman was given the honor / duty of having “discovered” (or being allowed to re-discover) quasi-crystals on April 8, 1982 with an Aluminum-Manganese alloy (Al6Mn) that began in a molten liquid state and was then cooled off very quickly. Crystals in the shape of an icosahedron were produced, as determined by the X-ray diffraction diagram that was seen, similar to the image below. Schechtman’s data was not even published until November 1984! In the image to the right of Figure 3.4, we can clearly see a number of pentagons, indicating the five-fold symmetry of the icosahedron: "click" image to see multimedia Figure 3.4 – The Icosahedron (L) and its X-ray diffraction diagram from a quasi-crystal formation (R). As we said, with the advent of quasi-crystals, both the dodecahedron and icosahedron appear, along with other unusual geometric forms, completing the appearance of all five of the Platonic Solids in the molecular realm in some way. Both the dodecahedron and icosahedron possess elements of five-fold symmetry with their pentagonal structures. Figure 3.5, from An Pang Tsai of NRIM in Tsukuba, Japan, shows an Aluminum-Copper-Iron quasi-crystal alloy in the shape of a dodecahedron and an Aluminum-Nickel-Cobalt alloy in the shape of a decagonal (10-sided) prism: Figure 3.5 – Dodecahedral (L) and decagonal prism (R) quasi-crystals created by An Pang Tsai of NRIM. The problem here is that you cannot create such crystals by using single atoms bound together, yet as we can see in the photographs, they are very real. The key problem for scientists, then, is how to explain and define the process by which these crystals are forming. According to A.L. Mackay, one of the ways to include five-fold symmetry in a crystallographic definition is “Abandonment of Atomicity:” Fractal structures with five-fold axes everywhere require that atoms of finite size be abandoned. This is not a rational assumption to the crystallographers of the world, but the mathematicians are free to explore it. [emphasis added] What this suggests is that similar to microclusters, quasi-crystals appear to not have individual atoms anymore, but rather that the atoms have merged into a unity throughout the entire crystal. While this may seem impossible for crystallographers to believe, it is actually among the simplest of A.L. Mackay’s four potential solutions to the problem, as it involves simple three-dimensional geometry and correlates with our microcluster observations. Again, since the crystals are very real, the only major hurdle to cross is our fixation on the belief that atoms are made of particles. Another related example is seen with the Bose-Einstein Condensate, which was first theorized in 1925 by Albert Einstein and Satyendranath Bose, and was first demonstrated in a gas in 1995. In short, a Bose-Einstein Condensate is a large group of atoms that behaves as if it were one single “particle,” with each constituent atom appearing to simultaneously occupy all of space and all of time throughout the entire structure. All the atoms are measured to vibrate at the exact same frequency and travel at the same speed, and all appear to be located in the same area of space. Rigorously, the various parts of the system act as a unified whole, losing all signs of individuality. It is this very property that is required for a “superconductor” to exist. (A superconductor is a substance that conducts electricity with no loss of current.) Typically, the Bose-Einstein condensate is only able to be formed at extremely low temperatures. However, we seem to be observing a similar process occurring in microclusters and quasi-crystals, where there is no longer a sense of individual atomic identity. Interestingly, yet another similar process is at work with laser light, known as “coherent” light. In the case of the laser, the entire light beam behaves as if it were one single “photon” in space and time – there is no way to differentiate individual photons in the laser beam. It is interesting to note that lasers, superconductors and quasi-crystals were all found in recovered ET technologies since the 1940s. This obviously introduces a whole new world of quantum physics to the discussion table. In time, it appears that quasi-crystals and Bose-Einstein condensates will be much more widely used and understood as examples of how we had gone astray in our “particle”-based quantum thinking. Furthermore, British physicist Herbert Froehlich proposed in the late 1960’s that living systems frequently behave as Bose-Einstein condensates, suggesting a larger-scale order that is at work. We will discuss this in later chapters that will deal with aetheric biology. 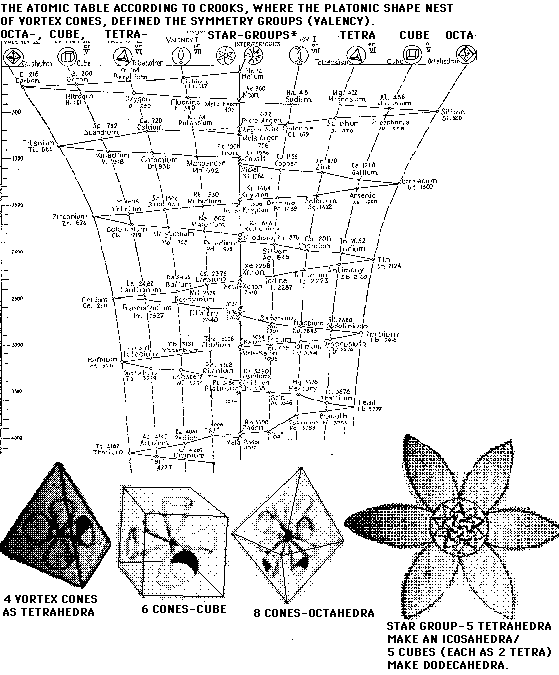Figure 3.6 – Dan Winter’s reprint of Sir William Crookes’ geometric Table of the Elements. Our next question concerns the “electron clouds” that have been seen in the atom. Both Rod Johnson and Dan Winter have noted that the teardrop-shaped “electron clouds” in the atom will all fit perfectly together with the faces of the Platonic Solids. Winter refers to the electron clouds as “vortex cones,” and Figure 3.6 is an unfortunately illegible copy of the Periodic Table of the Elements as originally devised by Sir William Crookes, a well-known and highly respected scientist from the early 20th century who later became an investigator into the field of parapsychology. At the bottom of the image, we see an illustration of how the “vortex cones” fit on each face of the Platonic Solids. (It appears that a more legible copy of Figure 3.5 may exist in one of Winter’s earlier books. Some of the element names can be made out when viewing the image at full size, and the others can be inferred by their position relative to the known Periodic Table of the Elements. The chart is obviously read from the top down, and the first element that is written out below the two circles in the center is Helium, and the line then moves to each successive element. The scale to the left is a series of degree measurements, beginning with 0 at the top line and counting by units of 10° for each line. The degree numbers written in on the scale are 50, 100, 150, 200, 250, 300, 350 and 400. This appears to indicate that Sir Crookes’ theory involved set angular rotations or translations of the elements in terms of their geometry as we move from one element to the next. We can see that the wave is mostly straight, but at times there are “dips” in the line that appear to correspond to larger angular rotations that must be made.) If we think back to what Dr. Aspden wrote about Platonic Solids in the aether, he stated that they act as “fluid crystals,” meaning that they can behave as a solid and as a liquid at the same time. Thus, once we understand that electron clouds are all being positioned by invisible Platonic Solids, it becomes much easier to see how crystals are being formed and even how quasi-crystals could be made. There are “nests” of Platonic Solids in the atom, one solid for each major sphere in the “nest”, just as there are “nests” of electron clouds at different levels of valence that all co-exist. The Platonic Solids form an energetic structure and framework that the aetheric energy must flow through as it rushes towards the low-pressure positive center of the atom. Thus, we see each face of the Solids acting as a funnel that the flowing energy must pass through, creating what Winter called “vortex cones.” With the necessary context in place, Johnson’s concepts of Platonic symmetry within the structure of atoms and molecules in the next chapter should not seem as strange to us now as they would to most people. Given what we have seen with the comprehensive research that has gone on, especially with quasi-crystal engineering, it appears that this information is already in use by humanity in certain circles. REFERENCES 1. Aspden, Harold. Energy Science Tutorial #5. 1997. URL: http://www.energyscience.co.uk/tu/tu05.htm 2. Crane, Oliver et al. Central Oscillator and Space-Time Quanta Medium. Universal Expert Publishers, June 2000, English Edition. ISBN 3-9521259-2-X 3. Duncan, Michael A. and Rouvray, Dennis H. Microclusters. Scientific American Magazine, December 1989. 4. Fouche, Edgar. Secret Government Technology. Fouche Media Associates, Copyright 1998/99. URL: http://fouchemedia.com/arap/speech.htm 5. Hudson, David. (ORMUS Elements) URL: http://www.subtleenergies.com 6. Kooiman, John. TR-3B Antigravity Physics Explained. 2000. URL:http://www.fouchemedia.com/Kooiman.htm 7. Mishin, A.M. (Levels of aetheric density) URL: http://alexfrolov.narod.ru/chernetsky.htm 8. Winter, Dan. Braiding DNA: Is Emotion the Weaver? 1999. URL: http://soulinvitation.com/braidingDNA/BraidingDNA.html 9. Wolff, Milo. Exploring the Physics of the Unknown Universe. Technotran Press, Manhattan Beach, CA, 1990. ISBN 0-9627787-0-2. URL: http://members.tripod.com/mwolff Return to Quantum Return to Geometria Sagrada